Dolt is the world's first version controlled SQL database. A MySQL-compatible SQL server, it supports Git-like version control primitives such as branch, merge, commit, diff, stash and rebase, as well as remote-based operations like push, pull and clone.

In the same way that Git is based on storing the versioned file trees as content-addressed Merkle DAGs, Dolt stores database data in a content-addressed Merkle DAG based on a search tree called a Polly Tree. We've written quite a bit about Prolly Trees in the past. Recently a colleague asked me "Why are Prolly Trees typically balanced?", and I thought it was an interesting question. So this blog post is just a short description of what factors affect a Prolly Tree's "balance" and some ways to think about how balanced your Prolly Trees are.

A Quick Recap

As a quick overview, let us recall that a Prolly Tree is an indexed data structure for storing ordered key-value pairs. If we have all of the key-value pairs in order, then we run a probabilistic value-based chunking algorithm on the sequence of key-value pairs, cutting the serialized sequence into a series of chunks. Each chunk covers a distinct range of the key-value pairs, and we can assign the chunk a content-addressed address by, for example, hashing its serialized contents.

Assuming there is more than one chunk resulting from this process, we next create the first internal layer of the tree by creating a new sequence of key-value pairs. There is a single entry in this layer for each chunk in the next lower layer. Its key is the same as the key of the last value in that chunk, while its value is the content address of the chunk itself. We perform this operation recursively, applying the probabilitistic chunker to each internal layer, until the probabilistic chunker generates exactly one chunk for the current layer. In that case, that chunk is the root of the Prolly Tree and its address can be recorded as the content address of the entire search structure.

So the height of the tree is however many layers we had to chunk in order to arrive at just a single chunk for the root of the tree. The tree grows in height exactly when a newly inserted record causes a cascade of new chunks at every internal level and the root itself ends up splitting into more than one chunk.

In general, the height of a Prolly Tree is highly dependent on the data and the properties of the content-addressed chunking which is being used. For example, you might have the following concrete parameters, which are similar to Dolt's: (1) the chunker targets an average chunk size of ~4KB, (2) chunk addresses consume 20-bytes. Let's say, for the sake of exposition, we are storing a table like:

CREATE TALBE vals (
  id BIGINT PRIMARY KEY,
  val BIGINT
)

In this case, each key-value pair is two 64-bit intergers, and so takes up 16 bytes in total. We would expect to fit slighly less than 256 of them in each leaf node, accounting for some serialization overhead. For each internal node, we will need 8 + 20 bytes for each key-value pair, because the chunk addresses themselves are 20 bytes. That means our average branching factor on levels of height greater than 1 will be slightly less than 146, again accounting for some overhead associated with serialization. On average, each chunk within the first internal layer of the tree will reach 146 * 256 = 37,376 entries, while each chunk within the second internal layer of the tree will reach 146 * 146 * 256 = 5,456,896 entries.

Similar calculations can be done for arbitrary schemas. For many types of data, the most important factors are the average size of the entries and the average size of the primary key — the entries themselves are stored in full in the leaves, and one primary key + 20 bytes are stored per chunk in the next lower level, for each entry in an internal level.

Another Take on Balanced

Prolly Trees are somewhat "balanced" by construction—the path to every leaf entry passes through the exact same number of chunks. If we are used to looking at data structures with fixed node sizes, this can be misleading. In the asymptotic analysis of data structures optimized for external storage, we are often interested in the number of block transfers—a fixed size block of storage which is loaded from an I/O device into memory—which are necessary to perform an operation. For Prolly Trees, it is important to be careful here, and to take notice of where we have deviated from other traditional structures with fixed-size entries such as B+-trees.

Above we looked at a content-dependent chunker that targeted an average chunk size of 4KB, which allowed us to calculate the average height of tree given its schema and the number of entries. This in turn tells us how many chunks we need to walk through to get to any given leaf entry. It does not, however, tell us us the average number of key comparisons we need to do or the average number of block transfers, for a given fixed block size, we need to do. To know that, we need to know more about the distribution of the sizes of the chunks which the chunker creates.

To see why the distribution matters, imagine the following degenerate scenario. We are interested in analyzing the search performance of a Prolly Tree with regards to block transfers. For the purpose of this analysis, we assume a block transfer is 4KB. Imagine that we have the following tree:

1. The tree has 32,768 entries, each taking up 16 bytes.

2. The tree is of height 2—it has leaves as well as its single internal layer, its root, which is exactly one chunk and which references all of its leaf chunks.

3. The leaves are chunked into 128 chunks.

4. 127 of those chunks have exactly one entry, taking up 16 bytes.

5. The other leaf chunk has the remaining 32,641 entries. It takes up 522,256 bytes.

6. Its root node—its one internal node—has 128 entries pointing to each of the 128 leaves.

This tree has leaf chunks with an average size of 4KB. Every path from root to leaf in this tree goes through exactly two chunks. But this tree is obviously massively imbalanced. The cost to access 127 of the entries is exactly two block transfers, while the cost to access any of the remaining 32,641 entries is 129 block transfers. That's a massive number of I/Os and a lot of search work within the giant chunk which we have to perform to access the majority of the data in the tree. With more evenly-sized chunks, the maximum cost to access any leaf would be exactly two block transfers, wich much less overhead on the searches within the accessed chunks as well.

The example demonstrates that in order to talk about balance in a Prolly Tree, we have to analyze the distribution of the sizes of the chunks which the content-dependent chunker produces.

Dolt's Chunk Size Distribution

We have previously written about Dolt's chunk size distribution. Dolt's chunker takes the existing size of the chunk into account when considering the likelihood of splitting a chunk at a particular point. The result is that Dolt's chunk sizes are much more smoothly distributed than the above counter example, or even than a static-chunking approach which tends to generate chunks with a geometric distribution on their sizes.

As explained in the previous blog post, we can target any distribution for the sizes of the resulting chunks. By some analysis, the less variance there is in the underlying targetted distribution, the more "balanced" the resulting Prolly Tree will actually be. But picking a distribution that is less locally content-dependent has tradeoffs. We rely on resychronizing with the chunk boundaries of the existing tree when we are mutating it in order to keep the cost of mutations O(height of tree * size of mutation) as opposed to O(size of tree). Resychnronizing is also critical to efficient diff and merge across versions of the Prolly Tree and for efficient structural sharing. The stricter we make the output sizes of the chunker, the longer it will take for certain kinds of mutations to resychronize with the previous versions of the Prolly Tree. As a result, we want to allow for some flexibility in how we chunk, while still keeping the bulk of our chunks within a pretty narrow range of sizes.

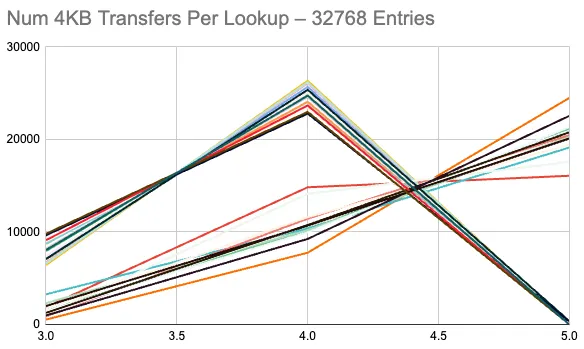
Dolt uses a truncated Weibull distribution as the target for its Prolly Tree chunker's chunk sizes. To analyze how balanced its trees were, I ran an experiment where I generated many random tables of the above schema and I counted how many 4KB block transfers it would take to access each entry in the tree. Here is the distribution for the number of block transfers to look up each entry in each of the 32 trees:

And this is the composite histogram across all 32 of the trees:

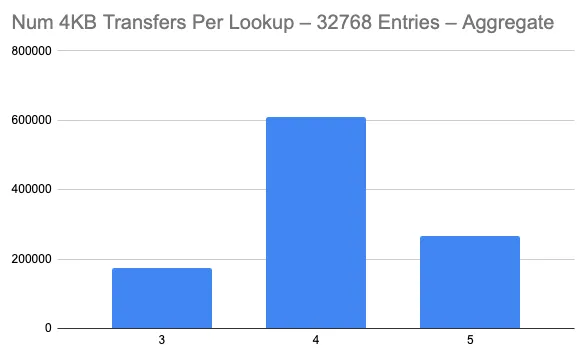
Because of the overhead associated with serialization and because Dolt's chunker tends to target chunks slightly larger then 4KB, the majority of these trees are of depth 3, with a two or three entry root chunk. Some of the trees are of depth 2 with a much larger root chunk. You can see that a few of the trees have a median transfer count of 5 blocks for a lookup, while the majority have a median of 4 blocks. The trees where many lookups take 5 block transfers typically have a depth of 3 and a few large internal nodes on their inner layer, so that they often pay 3 transfers before they get to the leaf.

As the tree gets bigger, noise from the randomness associated with chunking tends to even out. Here are similar plots for 8 different trees, each with 8,388,608 entries.

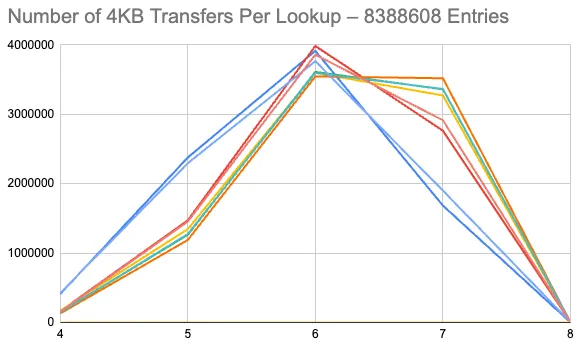
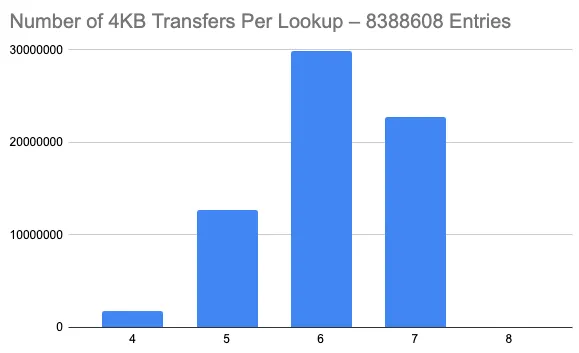
These trees all end up being of height 4, with the root node having 3 or 4 entries.

Conclusion

As you can see, in general there are no extreme outliers for accessing one part of a Prolly Tree versus another, and the Prolly Tree in general does a pretty good job of minimizing block transfers to access any given part of the tree.

As we saw, because nodes are not of a uniform size in a Prolly Tree, the appropriate things to look for when considering its balance is the distribution of its node sizes, and not its height. By construction, the path from the root to any given leaf entry is always the same length in a Prolly Tree.