Dolt is a next-generation SQL database with Git-like version control features. It's the only SQL database with branches that you can diff, merge, and sync. The core of Dolt's data model is a Merkle Tree index called a Prolly Tree. Prolly Trees draw on design concepts from databases, content-addressable storage, and version control systems. Combining these primitives creates a unique Merkle-based storage-engine that sets Dolt apart from other relational databases. Today we're doing a deep dive on Prolly Trees, content-addressable storage, and how we've leveraged these techniques to create a modern transactional database.

Prolly Trees 101

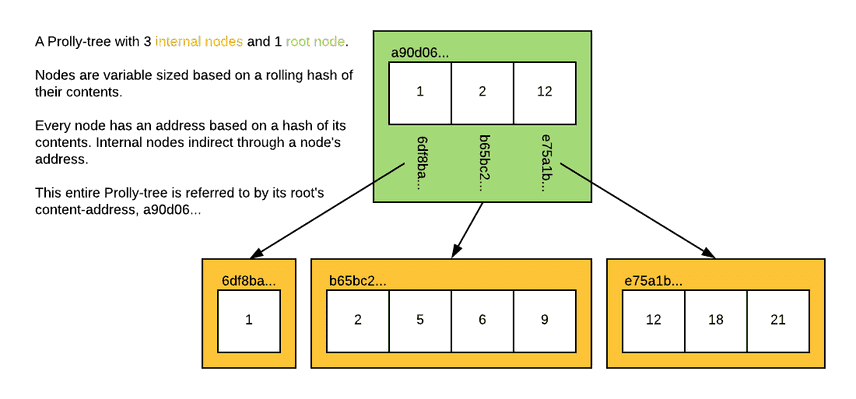
Prolly Trees originated in Noms, an open-source datastore developed by Attic-Labs. Noms used a schemaless data model, but Prolly Trees similarity to B+ Trees make them a general-purpose database index. The key difference between these two indexes is that nodes in a Prolly Tree are referenced by their content-address rather than a file-pointer. This network of hashes forms a Merkle Tree capable of comparing index revisions with an efficient diff algorithm.

Conceptually, the structure of a Prolly Tree is quite simple. On the read-path, accessing key-value pairs works as it does in B-tree; accessing index diffs works as it does in a Merkle-Tree. In order to optimize for both of these access patterns, we require that all mutations to the tree are history-independent. This invariant requires that a tree's structure must be a deterministic function of the contents of the tree. Said another way, a set of elements must always form the same tree, regardless of the order they were inserted in.

Prolly Trees are constructed and mutated from the bottom up. Key-value pairs are sorted into a sequence that forms level 0 of the tree. This sequence is then divided into discrete leaf nodes using a "chunking" algorithm that takes the key-value sequence as input and gives a boolean output of whether the current "chunk" should end after the current key-value pair. Next, a new sequence of key-value pairs is created from the last key of each leaf node and the content-address of that node. This sequence is again chunked using a rolling-hash and forms level 1 of the tree. This process continues until we reach a level with a single root chunk.

For Prolly Trees, chunk boundaries occurs when the values of a rolling-hash function matches a specific, low-probability pattern. Using a rolling-hash in this way is referred to as content-defined-chunking. Rolling-hash functions are well-suited to this problem because they are both deterministic (ie history-independent) and make decisions locally. As a counter-example, it would also be purely deterministic and history-independent to create fixed-size chunks. However, any insertion into such a sequence would cause a cascade of boundary changes through the postfix of the sequence. It's vital that any chunking algorithm be resilient to this boundary-shift problem. Maintaining stable chunk boundaries between revisions minimizes write-amplification and maximizes structural-sharing.

Content-Addressable Storage

If rolling-hash functions and content-defined chunking sounds familiar, you might recognize the terms from file-backup utilities like Rsync. Rsync performs differential backup. using content-defined chunking. Each chunk's content address becomes a deterministic short-hand for the file segment, meaning that different file revisions can be compared and patched by processing only the portions of the file that differ between revisions.

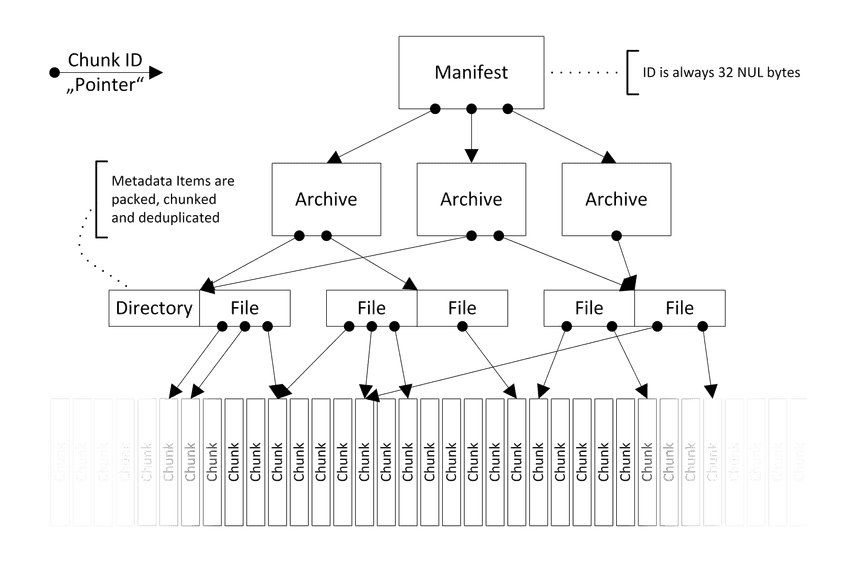
Later archive tools like Attic and Borg extended these concepts perform backups on entire file-systems. By chunking both files and directories, they built up content-addressed object graphs that could both synchronize data and expose a versioning API to access revision history. In fact, the hierarchical structure of Borg's data model bears some resemblance to that of a Prolly-Tree:

Noms represented a fundamental shift for content-addressable storage. By applying chunking to key-value stores, rather than file-systems, Noms made the technology both more scalable and more ergonomic. Exposing a key-value interface shifted the focus from data-backup to versioning and synchronization at the application layer.

Optimizing for OLTP

Dolt is a SQL database with Git-like version control. Since its creation, Dolt has used Noms for its storage layer. Up to this point, we've described Prolly Trees as they were originally implemented in Noms. As we've built Dolt, we've incrementally optimized Prolly Trees for our use case, but we eventually reached a point of diminishing returns. To address this, we're developing a new purpose-built storage engine designed around OLTP access patterns. For the rest of this post, we'll cover recent design changes we've made to our implementation and to our chunking algorithm in particular. The design changes were motivated by three issues we observed when using Prolly Trees in an OLTP context:

• variance in the chunk size distribution
• chunking stability for low-entropy inputs
• chunking performance for small updates

Chunk Size Variance

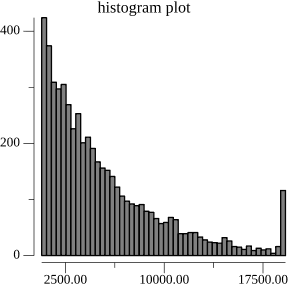
As mentioned above, Noms chunks trees by matching the value of rolling-hash against a static, low-probability pattern. We'll call this approach static-chunking. The pattern chosen dictates the average chunk size in the final tree. A pattern that occurs once in every 4096 samples will produce a distribution of chunks that are on average 4096 bytes large. In particular, the chunk sizes form a geometric distribution. We can see this in practice by visualizing the chunk sizes distribution of 1 million random key-value pairs:

As you might expect, this is not an ideal distribution. On the read-path, the variance in size creates unpredictable IO performance when reading chunks from disk. The story is even worse on the write-path. Prolly Trees are copy-on-write indexes: each chunk must first be copied before it can be mutated. Large chunks in the tail of the distribution are very expensive to copy and mutate. Despite these large chunks being somewhat uncommon, the greater key cardinality of these chunks means that they are much more likely to be accessed than smaller chunks.

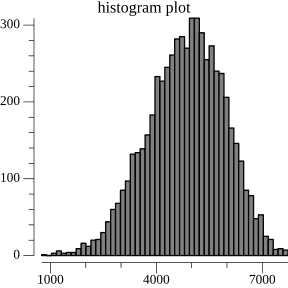
Ideally we'd like a chunk size distribution with minimal variance and predictable performance, but our chunking function must still be deterministic and resilient to the boundary-shift problem. A simple solution is to use the size of the current chunk as an input into the chunking function. The intuition is simple: if the probability of chunk boundary increases with the size of the current chunk, we will reduce the occurrence of both very-small and very-large chunks.

Implementing this pattern is also straight-forward. Given a target probability-distribution-function (PDF), we use its associated cumulative-distribution-function (CDF) to decide the probability we should split a chunk of size x. Specifically, we use the formula (CDF(end) - CDF(start)) / (1 - CDF(start)) to calculate the target probability. We then use the output of the hash function as a random variable to decide whether to end the current chunk and start a new one. Concretely: if the current chunk size is 2000 bytes the probability of triggering a boundary by appending a 64 byte key-value pair is (CDF(2064) - CDF(2000) / 1 - CDF(2000). Using this general approach we're able to choose any target probability distribution. We can visualize the difference in output distribution using the same dataset as before:

Rolling-Hash Stability

Classic content-defined-chunking algorithms are input agnostic; they process files as opaque byte streams and use the entropy within the stream to seed the rolling-hash function. This creates a problem for Prolly Tree indexes whose ordered contents naturally have lower entropy. This is compounded by the fact that popular rolling-hash functions such as buzhash have poor output quality on sorted or low entropy input. In Dolt, this manifests as rolling-hash output that fails to trigger chunk boundaries, leading to massive chunks.

What we need is a stronger hash function, and we can leverage the key-value structure of our tree to get exactly that. Rather than hashing key-value pairs as a byte stream, we can simply hash the discrete byte strings of the key-value pair. Index keys are necessarily unique, making them an appropriate source of entropy for our chunker given a sufficiently strong hash function. This approach is also faster that a rolling-hash function because the number of hashes we need to compute is now proportional to the number of key-value pairs in a node, not the number of bytes. One subtlety of this change is that we're now chunking nodes with an average number of key-values pairs rather than an average size, but this difference disappears after using the dynamic probability pattern described earlier.

Chunking Performance

The key-hashing approach was first proposed by Mikeal Rogers of IPFS in this github issue. The initial proposal was to compute a hash from the byte strings of the key and value. However, modifying this approach to compute a hash over only the key has further advantages. Consider a Dolt table with the following schema:

create table fixed (
    pk primary key int,
    c0 float,
    c1 char(20),
)

Row data for this table is stored in a clustered index where pk forms the key tuple and c0, c1 form the value tuple. Because this schema contains only fixed-width column types, any in-place UPDATE queries to this table are guaranteed to not shift a chunk boundary. This is true both for leaf nodes and for internal nodes where chunk address pointers are also fixed-width fields. In fact, for any given index in Dolt, most writes will be dominated by these fixed-width updates. For example, an insert into a leaf node adds a new key tuple and changes the overall size of leaf node, but assuming a low-probability boundary shift, each higher level of the Prolly Tree can be edited in-place. In this way, key-hashing is well-suited to OLTP write patterns where small, frequent index updates are the norm.

This new Prolly Tree implementation is still experimental, but we're releasing an early version to users to gather feedback and to preview future performance gains. It's currently behind a feature flag, but you can turn it on by setting the environment variable DOLT_DEFAULT_BIN_FORMAT=__DOLT_1__ and creating a new database with dolt init.

Wrapping Up

Databases, and data systems at large, are defined by their core architecture. Major advancements in database tech often result from the introduction of novel data-structures or algorithms. The advent of B-Trees in the mid 20th revolutionized the scale of early data systems. Decades later, Git revolutionized version-control software using a Merkle-based storage layer. We're biased, but we hope that Prolly Trees can provide a similar advancement for transactional databases. We're certainly interested to hear your thoughts. If you have any questions, or if you want to nerd-out about databases hit us up on Discord!