tl,dr: We’re adding a new algorithm for dolt merge that should massively speed up merges when two branches modify the same table but different regions of the primary key-space. No action is required in order to benefit from this change, although currently this algorithm will only be used when the table has no schema changes, secondary indexes, or constraint checks.#
“Dolt is Git for Data.”#
We say this a lot. It means that Dolt has all of Git’s nifty version control features, but for your database instead of your files. You can view commit history, make new branches, and work on those branches in parallel. When you’re ready, you can merge the branches back together, creating a branch that contains the combined changes from both its parents. Anything you can do with Git to version control your files, we want you to be able to do in Dolt to version control your database.
Unsurprisingly, Dolt has a lot of similarities to Git under the hood. One of those similarities is how both Git and Dolt store content internally, and how this impacts merges.
How Git Does Merges#
If you’ve ever peeked under Git’s hood, then you might know that Git represents your file system as a Merkle tree. Every file and directory in Git has a hash, defined by its contents. Directories contain the names and hashes of all their child files. This is great because it makes it easy to detect which parts of the file system have changed and which parts haven’t.
So for example, a file system stored in Git might look like this:
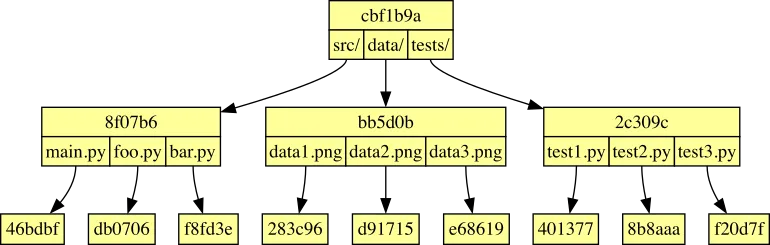
After two different branches make their own changes to this file system, those two branches might end up looking like this:
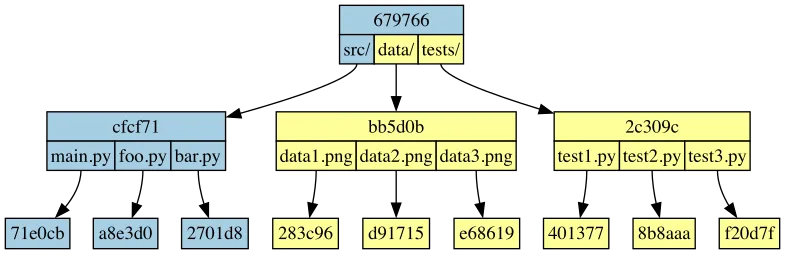
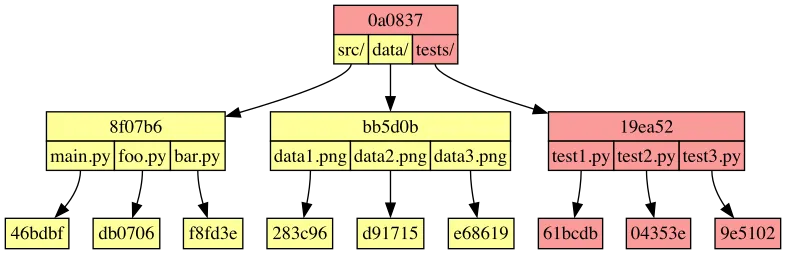
After merging these branches, the final tree looks like this:
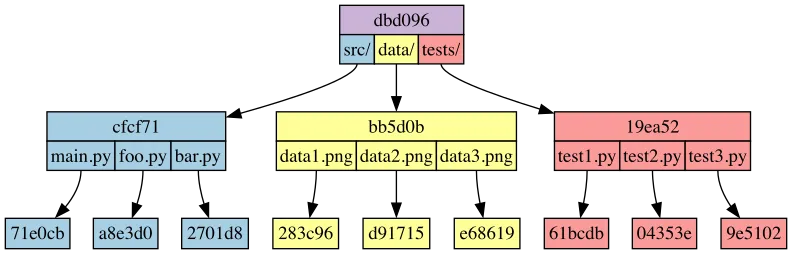
If a file or directory has the same hash at two different commits, we know that the contents of that file or directory are the same in both commits. Git can leverage this fact in order to merge branches very efficiently. Merging in Git works recursively, starting with the hash for the root directory and only recursing into subdirectories when actually necessary. So Git merging works like this pseudocode:
def merge(directory):
mergedDirectory = {}
for fileName in directory:
leftHash, rightHash, ancestorHash = getHashes(fileName)
if leftHash == rightHash:
result[fileName] = leftHash
else if leftHash == ancestorHash:
result[fileName] = rightHash
else if rightHash == ancestorHash:
result[fileName] = leftHash
else:
# a conflict
if isDirectory(fileName):
# resolve directory conflict by merging recursively
result[fileName] = merge(fileName)
else:
# attempt to resolve file conflicts by
result[fileName] = resolveConflict(fileName)
return mergedDirectoryThe real algorithm has to handle things like files being added and deleted, but this gets the gist across. With this method, if both branches never modify the same subdirectory, the merge is very efficient. This is true even if those subdirectories had tens of thousands of files changed. It doesn’t matter how many changes exist on the lower levels of the tree, because merge algorithm never needs to recurse into the tree.
How Dolt Does Merges#
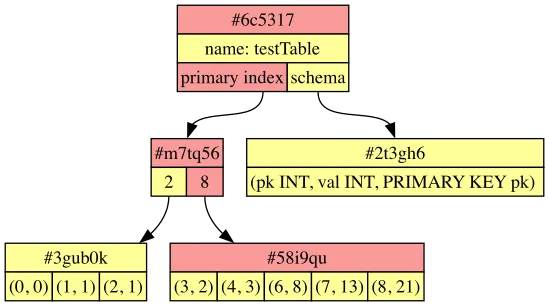
Now let’s look at how Dolt stores your database tables. Dolt also uses Merkle trees to represent your data. More precisely, we use a special kind of Merkle tree called a Prolly Tree, which stores an ordered list of key-value pairs in a predictable, self-balancing way. At a specific commit, your database might look like this:
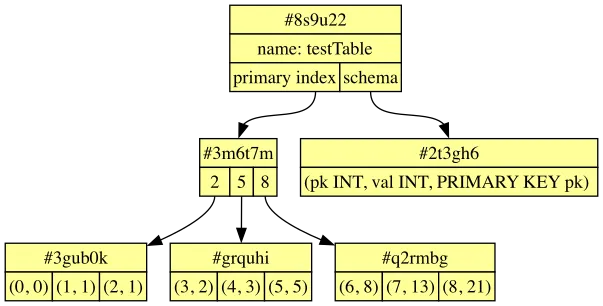
Each node in the primary index represents a range of keys. Within each non-leaf node, its children are labeled with the maximum key that appears in that child.
Like before, let’s imagine that two different branches both diverge from this commit:
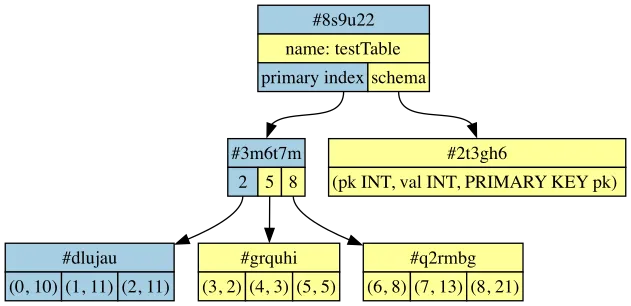
Given the similarities, you might assume that Dolt can merge changes to tables the exact same way that Git merges changes to directories.
I assumed that too. But I was wrong.
Instead, Dolt’s original algorithm for merging a table looked like this:
- Find all rows that changed between “their” branch and the common ancestor.
- Find all rows that changed between “our” branch and the common ancestor, and check whether any of those conflict with the changes in “theirs”.
- For each row that changed in “theirs” that doesn’t have a conflict, update that row in “ours” to match it.
This produces the merged tree, but it has a major downside: it scales in runtime with the number of changed rows on both sides of the merge. This means that if either side changed many rows, the merge will be very slow. If the branches diverged from each other a long time ago, merging will be very expensive, even if one of the branches only has a small number of changes.1
For these reasons, “long-lived branches” as a feature had a pretty noticeable performance cost.
When I first discovered this limitation, I didn’t understand why it existed. And looking at the trees in the example above, it seems like it would be easy to perform the merge without needing to look at the individual row changes stored in the leaf nodes of the tree.
And in this specific example, it would be easy. But merging Prolly trees in general is hard, for the simple reason that node boundaries can shift, causing the same key to appear in different nodes even when it hasn’t changed.
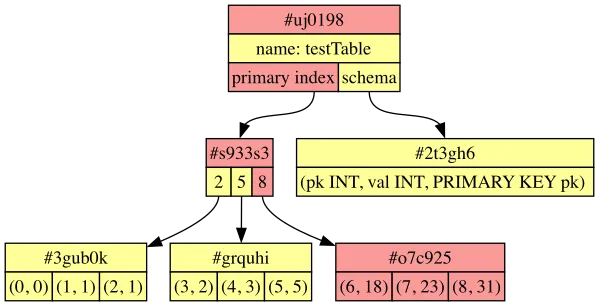
Consider these two branches, which have the same common ancestor as the above example. Here, both commits removed a single row, causing two of the leaf nodes to combine:
Now look at key 3. This key exists in all three trees. Its value has not changed, and there’s clearly no merge conflict. But the path through the tree to reach the key is very different, and the only way to determine that there’s no conflict is to fully load the leaf nodes containing that key and compare the individual rows.
Because of this, it’s tricky to merge Prolly trees in all but this simplest of cases. But tricky doesn’t mean impossible, and now I’m proud to announce that Dolt can leverage the structure of tables in storage in order to perform merges on tree nodes without needing to enumerate over every modified row.
The algorithm looks like this:
1. Diff both branches against their common ancestor to produce a stream of Patches#
For both branches, walk the tree to identify nodes that exist on the branch that didn’t exist in the common ancestor. From each of these nodes, we create a “patch”, which represents a change that could be applied to the ancestor tree to make that key range match the changed tree.
This process is interactive: at any point we can either ask for the next changed node, or split the current patch to recursively visit that node’s children to see which of those children were introduced by the branch.
2. Merge these streams into a single stream of non-overlapping Patches#
If we walk both trees simultaneously, at any point we have a single patch from each branch:
- If the patches don’t have overlapping key ranges, we record the one that comes first, then fetch the next patch from that branch.
- If they do have overlapping ranges, we split the patch that comes first, creating new smaller patches from its children nodes.
Once we finish walking both trees, we have recorded a list of non-overlapping patches that include every change introduced by either branch.
3. Apply Patches to produce the merged tree.#
By taking all of the recorded patches from one branch and applying them them to the other branch, we can produce the merged tree. In the best case, the node boundaries of the final tree are the same as the node boundaries in the original branches, applying a patch means simply inserting the node into the merged tree, without ever needing to load or inspect the node’s children. In cases where the node boundaries have shifted, we must recursively load the new node’s children and apply those instead. In the worst case we load and write every row into the new table, but the performance of this is no worse than the original merge algorithm.
This is glossing over a ton of detail, mostly to do with the many many corner cases:
- What happens if we finish walking one tree before we finish walking the other one?
- How do we correctly handle the case where the two trees have a different height?
- How do we detect when a node’s entire range has been deleted from one branch? Once we detect it, how do we record it?
- Once we reach the leaf nodes, we continue to compare those node’s children, but those children are individual key-value pairs instead of entire nodes. How does this change the logic?
- And most importantly, how do we apply a patch such that we correctly handle every possible case?
Detecting these corner cases and determining the correct behavior for each ended up being the bulk of the effort involved. As always, the devil was in the details.
There are currently some limitations on when we can apply tree-based merging, causing us to fall back on the original implementation. We won’t use tree-based merging if:
- The table has secondary indexes.
- The table has check constraints.
- The table schema has changed in one of the branches.
When these conditions are met, Dolt should automatically use the new merging algorithm. There’s no tradeoffs being made: the new algorithm should always be faster than the old one. We also expect that it should be possible to relax some of these conditions in the future, based on user need.
The Impact#
This isn’t just an X% speedup, but an asymptotic improvement in time complexity while still being no slower than the old algorithm in the worst case. Let’s look at a practical example that highlights the potential of the tree-aware merging approach:
Imagine using Dolt to build a database of metadata for a site like Wikipedia. (This is something we’re actually doing.). One possible approach would be to have multiple import processes running in parallel, where each process has its own branch that it populates, and these branches get reviewed and merged via a pull request. This isolated-branch plus manual-review approach is especially great if you’re using AI agents as part of your workflow.
Under the previous merge algorithm, if a branch adds five million rows to a table, and a concurrent change already added another five million rows to the table, merging your branch back into main will require processing all ten million rows that have changed since the two branches diverged.
But with tree-aware merging, the performance becomes dictated not by the number of changed rows, but by the number of new tree nodes that are created during the merge process. In the worst case where the changed rows are evenly distributed throughout the table, this number will be on the order of the number of changed rows. But if you’re smart and assigned each of your workers a non-overlapping region of your primary key space, the number of new tree nodes can be much, much smaller, even a single new chunk per row of the tree, which is log(n) in the number of rows.
Let’s simulate this. We’re going to create a table and populate two branches each with five millions rows2. I ran the following on my Apple M2 Pro with 32 GB of RAM:
import pymysql
import timeit
db = pymysql.connect(unix_socket="/tmp/mysql.sock", user="root", database="merge_test")
cur = db.cursor()
cur.execute("create table test(pk int primary key, val char(24);")
cur.execute("call dolt_commit('-Am', 'create test table');")
cur.execute("call dolt_branch('branch_two');")
cur.execute("call dolt_checkout('-b', 'branch_one');")
cur.executemany("insert into test values (%s, %s);", ((i, f"text_string_value{i:7}") for i in range(5000000)))
cur.execute("call dolt_commit('-Am', 'insert on branch_one');")
cur.execute("call dolt_checkout('branch_two');")
cur.executemany("insert into test values (%s, %s);", ((i, f"text_string_value{i:7}") for i in range(5000000, 10000000)))
cur.execute("call dolt_commit('-Am', 'insert on branch_two');")
# Time the merge:
timeit.timeit("""cur.execute("call dolt_merge('branch_one');")""", number = 1, globals=globals())A more important metric than the number of rows is the total amount of data being merged. In this schema, each row requires 32 bytes of storage. So five million rows means 16MB of data on both sides of the merge.
How long did this take:
| Dolt Version | Merge From | Merge Into | Average Runtime (s) |
|---|---|---|---|
| v1.56.0 | branch_one | branch_two | 9.046 |
| v1.56.0 | branch_two | branch_one | 9.143 |
| main (58a994) | branch_one | branch_two | 0.01195 |
| main (58a994) | branch_two | branch_one | 0.009743 |
That’s about a 1000x speedup. And as the amount of data being merged increases, the performance benefits continue to scale.
That’s All, Folks!#
As always, if you have any questions or comments, you can always join our Discord. If you use Dolt for version controlling your database and feel like your merges are slow, let us know about it and we can investigate whether or not your merges ought to be able to benefit from this. We take user feedback very seriously, which is why we have our 24 hour bug pledge.
Footnotes#
-
There are in theory optimizations that can tweak this approach to handle the case where one side has many fewer changes than the other. Unfortunately, identifying when to apply these optimizations requires counting the number of changes in both branches, which often defeats the entire purpose. Furthermore, this does nothing for the case where both branches have a large number of changes in different parts of the tree. ↩
-
We used a SQL command here instead of the
dolt mergecommand becausedolt mergeprints a summary at the end describing the number of rows changed by the merge. It turns out that in this situation, computing this summary actually dominates the runtime! ↩