Dolt is a SQL database that supports Git-like features, including branch, diff, merge, clone, push and pull. Dolt's SQL functionality is built on top of a SQL engine written in Golang. We've previously blogged about our first steps in optimizing joins in go-mysql-server. With increasing adoption of Dolt as an OLTP database for online applications and as parts of OLAP workflows, we've seen real life queries leaning on, and pushing the bounds of, Dolt's query optimizer. In this blog post, we highlight a few scaling bottlenecks our previous join optimization work ran into and recent improvements we've made to overcome them.

Overview

As noted in the previous post introducing our first pass at 3+ table indexed join search, a major piece of Dolt's query analyzer is a join search that tries to compute the best order in which to execute a series of joins within a query. The algorithm described there proceeds in two steps:

1. Find the lowest cost join order by taking into account table sizes

and available indexes for the given join conditions. This is done by orderTables in the extracted code.

2. Compute a tree of IndexedJoin nodes where the leaves appear in

the lowest cost order and the available indexes are used as intended.

As the capabilities of the engine grow and our users throw increasingly complicated queries at it, they quickly realized that, as presented, those two steps have some pretty intense assymptotics in the number of tables being joined. In particular, step one visits every possible permutation of the tables, which is O(n!). 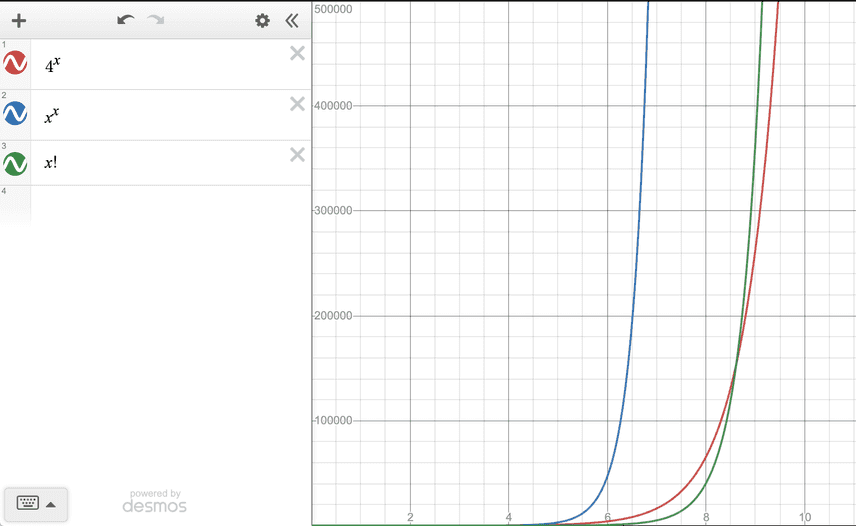Step two, which involved a naive recursive exhaustive search of every possible tree, and checking if it happened to meet our preferred join order, was O(n^n). Both of those factors need to be improved, but x^x is particularly burdensome .

Because of how the search was implemented, the effective limit of how many tables we could join in a single query was 6 or 7. That simply wasn't going to work for many useful queries. We set out to improve our n^n factor in particular.

Knowing What You're Looking For

A basic optimization that was available in the previous join search implementation is that it generated and visited lots of join plans that did not match the desired table order that had already been calculated as being minimal cost. Those trees were never going to be accepted by the search, but there was no attempt to prune them early.

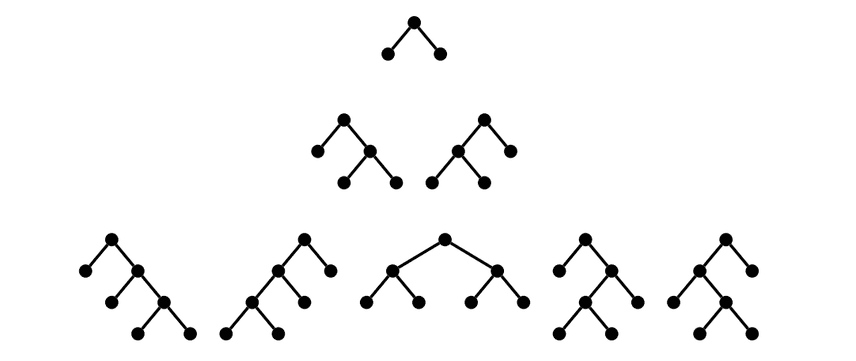
Generating every possible subtree and looking for one that matches your criteria is an easy to understand and implement approach, but in this case we could do a lot better with very minimal changes. The basic observation is, we don't need to generate every possible join tree and take the first matching one. Instead, we can reduce our work by only generating every possible subtree that a priori matches the desired table order. The problem reduces to generating every possible complete binary tree and making the leaves of the binary tree the tables in the given order.

¹

The recursive solution is pretty straightforward. Given a variant of our joinSearchNode from before:

type joinSearchNode struct {
    table string            // empty if this is an internal node
    left  *joinSearchNode   // nil if this is a leaf node
    right *joinSearchNode   // nil if this is a leaf node
}

and a list of table names for the leaves tables []string. We can construct our trees as follows:

func allJoinSearchTrees(tables []string) []joinSearchNode {
    if len(tables) == 0 {
        return nil
    }
    if len(tables) == 1 {
        // A single table becomes a leaf.
        return []joinSearchNode{joinSearchNode{table: tables[0]}}
    }
    var res []joinSearchNode
    for i := 1; i < len(tables); i++ {
        for _, left := range allJoinSearchTrees(tables[:i]) {
            for _, right := range allJoinSearchTrees(tables[i:]) {
                res = append(res, joinSearchNode{left: &left, right: &right})
            }
        }
    }
    return res
}

Here we basically have two cases. If there is only a single table, then the only possible tree is the tree with one node where that table is the leaf. Otherwise, the solution is to treat each index into tables as a location for a root node in the binary search tree and compute all solutions with those nodes' left and right children as appropriate.

This recursive definition and the size of the result set is well studied in combinatorics. Known as the Catalan number, one of its applications listed on Wikipedia is "the number of different ways n + 1 factors can be completely parenthesized". That's exactly what we're doing here: choosing the order in which we will apply successive associative binary operators. The good news is that the Catalan number sequence grows O(3^n), which is much better than our previous n^n. It means that join tree construction is no longer the bottleneck, and instead the cost optimization, where we naively pay O(n!) considering every possible table ordering, is what we need to optimize next.

Fixing Some Bugs While We're Here

While we were doing this performance work, we came across a bug in the previous join search code that we needed to fix. As outlined in the previous blog post, the prior search code would treat left and right joins as table ordering constraints, but its tree search was actually too liberal when it came to constructing the order for the joins. It had a bug where it would sometimes commute a left or right join with an inner join. In a sequence of inner joins, every join is commutable with every other join, but when left and right joins are involved, their children are not—they represent structural constraints on the resulting join tree. A left or right join's children need to remain semantically equivalent in the resulting tree once the query plan is constructed.

Fixing this required us to change how we were representing ordering and search constraints in our search above. Instead of passing in a tables []string to our allJoinSearchTrees, we needed to pass an actual representation of the structural constraints on the tree itself. We ended up implementing our search around a new type:

type joinOrderNode struct {
    associative []joinOrderNode
    table       string
    left        *joinOrderNode
    right       *joinOrderNode
}

Here a node is either:

1. A leaf, with a non-empty table.

2. A structural constraint node, with non-nil left and right.

3. A slice of joinOrderNodes in associative, in which case we will

apply the parenthesization search as above.

Our parenthesization function just gets a little tweak for dealing with nodes of type (2), in which case it always inserts an internal node into the tree at that point.

func allJoinSearchTrees(node joinOrderNode) []joinSearchNode {
    if node.table != "" {
        return []joinSearchNode{joinSearchNode{table: node.table}}
    }
    var res []joinSearchNode
    if node.left != nil {
        for _, left := range allJoinSearchTrees(*node.left) {
            for _, right := range allJoinSearchTrees(*node.right) {
                res = append(res, joinSearchNode{left: &left, right: &right})
            }
        }
        return res
    }
    if len(node.associative) == 1 {
        return allJoinSearchTrees(node.associative[0])
    }
    for i := 1; i < len(node.associative); i++ {
        for _, left := range allJoinSearchTrees(joinOrderNode{associative: node.associative[:i]}) {
            for _, right := range allJoinSearchTrees(joinOrderNode{associative: node.associative[i:]}) {
                res = append(res, joinSearchNode{left: &left, right: &right})
            }
        }
    }
    return res
}

Results and Future Work

Dolt went from struggling to analyze seven table joins to comfortably handling ten table joins without join order hints. By adding join order hints, the most expensive part of the search can be skipped, but the parenthesization search is still exponential and it starts slowing down noticeably at around fifteen tables. The end results is that a lot of practical queries for our users become much more performant.

We still have a lot of work to do on analyzer performance and the execution performance of the resulting query plans—we went from being dominated by O(n^n) factor to being dominated by the O(n!) factor. We hope to add heuristics to our cost optimization search in the future, so that we can reliably find compelling orders in which to run a query without visiting all possible permutations of table orders. The parenthesization search describe above can also still be improved. It used to generate all possible join trees and it now generates only the trees with the appropriate table order. But it can also be changed to quickly backtrack when a tree that it is constructing cannot meet the constraints that will be imposed by the analyzer with regards to index utilization and join condition evaluation. The quicker we can prune large subtrees in the search, the less work will be wasted generating unusable results.

Overall we're happy to get these improvements into our user's hands, and we're excited to keep delivering improvements in this space in the future.