Dolt, the world's first SQL Database which has full version control properties, has a lot of interesting computer science lurking in its depths. Recently I've been writing about the Dolt storage system, and there is a very subtle bit buried in there about using a Prolly search on a large slice of 64 bit integers. The details aren't really that important, especially since the only reason that we didn't use a Binary search but used a Prolly search instead was because Aaron and I got nerd sniped.

Any Computer Science curriculum has an algorithms class. Mine was CS 102, and one of the things they beat to death was that searching is generally a O(log2(N)) problem; given that your data is sorted. Time and time again, I've seen this in some shape or another in my career - sort your information, store it, then expect a O(log2(N)) search time to look up anything. We generally accept O(log2(N)) search times because it turns out you can get through a lot of data with a logarithmic scaling factor. This system works because we can sort pretty much everything with a little thought.

What if we added and additional restrictions to our data which allow us to perform that lookup in constant time?!?

Is this a story of unnecessary optimization? Yes, yes it is. For this particular look up, the search is far far less time than the read time from disk. We are talking less than 0.1% of the total time. Is it a story of premature optimization? No, no it's not. That would imply that we were ignorant of the fact that our time was being wasted on the wrong thing. This is a story of the allure of a constant time algorithm; because it is too interesting to pass up.

Binary Search

The reason that search is generally O(log2(N)) is as follows.

Given a block of sorted data (we'll use uint32s), the classic Binary Search works because you can divide your entire data set in half with each step. Each subsequent step effectively cuts the search space in half again. Here is a binary search written in go:

func binarySearch(slice []uint32, target uint32) int {
	left := 0
	right := len(slice) - 1
	for left <= right {
		middle := left + (right-left)/2
		if slice[middle] == target {
			return middle // Found
		} else if slice[middle] < target {
			left = middle + 1 // Search right half
		} else {
			right = middle - 1 // Search left half
		}
	}
	return -1 // Not found
}

As an example, let's search for the value 61:

The first middle point is one step, and by the end of the loop you've ruled out half of the search space:

The second loop lands the middle point at index 11, which is higher than the target, so we move right over, having yet again removed half of the search space.

On the third and final loop, we find a match made in heaven:

Searching a set of 1M items is more of a real world scenario, but regardless of the size of the search space we can confidently say we are reducing the search space by exactly 1/2 with each iteration.

The time it takes to complete the search is effectively the number of loops required to get to the location where the value resides. To divide 1,000,000 repeatedly until you end up at the final answer takes on average ~19.93 steps. But if your data set doubles in size, you only need to perform ~20.93 steps to find your answer, which is only 5% more processing time despite your data growing by 100%. This is pretty neat, and really brings home how you can search a lot of data if you just have the requirement that your data is sorted before you attempt to search it.

Prolly Search

Can we do better than Binary Search? What if we add another requirement to our data that it be uniformly distributed? If we have the assumption that each value in the set has approximately the same difference between it's neighbor as all other elements, then we can make a more intelligent guess than simply cutting the set in half with each iteration.

Dolt uses "Prolly Trees" as a core building block, and that stands for "Probabilistic B-Tree". I'm coining a new term here: "Prolly Search" - short for "Probabilistic Search."

Here's the code:

func prollySearch(slice []int32, target int32) int {
	found := func() int {
		items := len(slice)
		if items == 0 {
			return 0
		}
		left, right := 0, items
		lo, hi := slice[0], slice[items-1]
		if target > hi {
			return right
		}
		if lo >= target {
			return left
		}
		for left < right {
			// Guess where the value prolly is, based on the target and the range of values.
			valRangeSz := int64(hi - lo)
			idxRangeSz := uint64(right - left - 1)
			shiftedTgt := target - lo
			offset := (int64(shiftedTgt) * int64(idxRangeSz)) / valRangeSz
			guess := int(offset) + left

			if slice[guess] < target {
				left = guess + 1
				// No need to update lo if left == items, since this loop will be ending.
				if left < items {
					lo = slice[left]
					if lo >= target {
						return left // Found it, or it doesn't exist.
					}
				}
			} else {
				right = guess
				hi = slice[right]
			}
		}
		return left
	}()
	// Above code plays well with the sort.Search interface,
	// but this check makes it's behavior identical to binarySearch above.
	if found < len(slice) && slice[found] == target {
		return found
	}
	return -1
}

This code above has the same general idea as the Binary Search - we are moving the left and right cursors as you narrow the search space. One subtle difference is that right is always 1 to the right. The reason for this is that we wanted to play nice with the sort.Search interface, which actually returns where to insert an element. Our actual implementation is for uint64 values, so we use 128 bit values for the guess. Using uint32 values allows us to use uint64s to avoid overflows, so the code here is a little easier to understand.

At the start, left and right are at the extremes.

Next we calculate the guess:

			valRangeSz := int64(hi - lo)                                   // valRangeSz = 97
			idxRangeSz := uint64(right - left - 1)                         // idxRangeSz = 15
			shiftedTgt := target - lo                                      // shiftedTgt = 60
			offset := (int64(shiftedTgt) * int64(idxRangeSz)) / valRangeSz // offset = 9
			guess := int(offset) + left                                    // guess = 9

slice[guess] is not less that target, so:

				right = guess                                             // right = 9
				hi = slice[right]                                         // hi = 61

Next we make a second guess:

			valRangeSz := int64(hi - lo)                                   // valRangeSz = 60
			idxRangeSz := uint64(right - left - 1)                         // idxRangeSz = 8
			shiftedTgt := target - lo                                      // shiftedTgt = 60
			offset := (int64(shiftedTgt) * int64(idxRangeSz)) / valRangeSz // offset = 8
			guess := int(offset) + left                                    // guess = 8

slice[guess] is less that target, so we bump the left value, and we've found the match.

				left = guess + 1                                           // left = 9

Using the same data and starting conditions, the prollySearch approach found its match in 2 steps, while the binarySearch required three steps. This is the critical piece for performance - more loops is more time. By taking an educated guess based on our knowledge of the data, we can hone in on the likely location more quickly than by simply cutting the set in half which each iteration.

Probably worth calling out that the code shown here has been highly optimized to avoid as many branch operations as possible. So, while we could say that the first guess landing on the perfect answer should be returned immediately, it turns out that branching for every special case like this slows down the implementation a lot. The Binary Search function is simple enough that it get's inlined by the compiler, so we had to work pretty hard to reduce the operations as much as possible. Aaron is way better at this than I am, so he deserves all the credit for this code.

Results

We ran some tests using data sets of increasing size. The datasets consisted of random integers which were sorted which is a decent representation of what our data looks like. We performed both searches which found values and searches which determined the value didn't exist in the set.

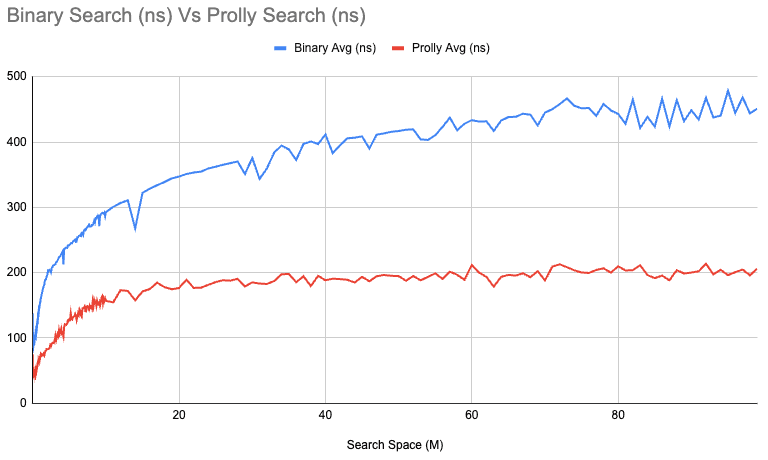
This is the average time required per search graphed by the number of elements searched:

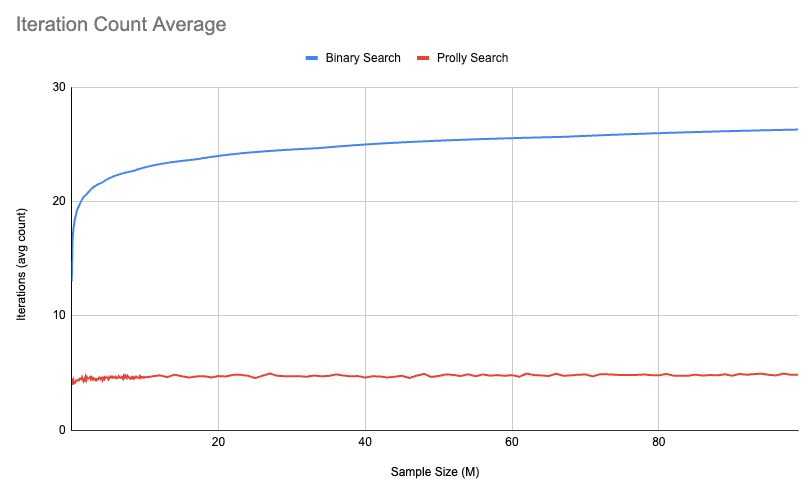
It looks like it could be constant, or approaching constant anyway. Another view of this is the average number of iterations required by each algorithm. Iterations are a more concrete measure of the work performed, while time can be impacted by many things. The average number of iterations pretty much exactly lines up with expectations:

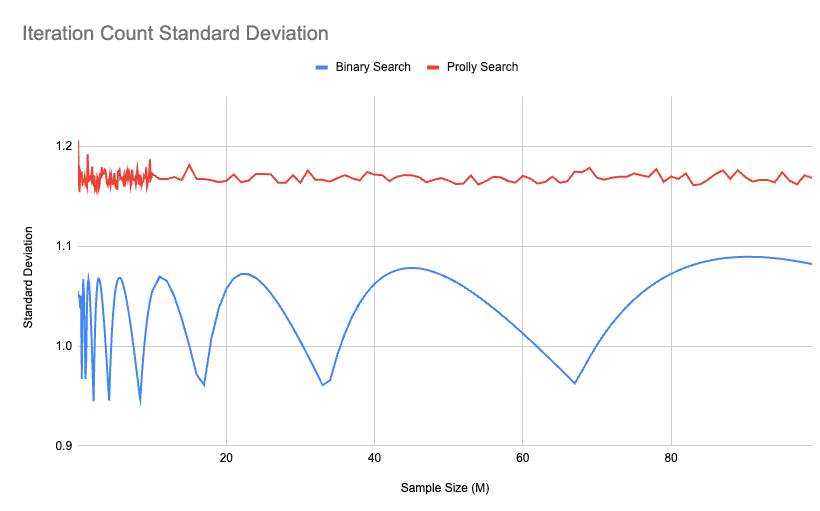
And finally, if we look at the standard deviation of each search within its set, we get this curious result:

Prolly Search's standard deviation is always higher than Binary Search. This means that even if it's faster on average, there are occasional outliers which take longer than others in the set. This makes sense because regardless of the data, Binary Search iterations can pretty mechanically be calculated. The waves of the Binary Search show clearly that the variability of search search is effected by the sample size. The dips in the Binary Search variance lands at multiples of 2, so 33 million, and 67 million are 2^25 and 2^26 respectively.

Prolly Search on the other hand depends on chance, and there are going to be situations where we guess wrong because no data is perfect. If data was perfect, then it would just be a mathematical function and I wouldn't have a job. On average, the number of iterations of Prolly Search is significantly better than for Binary Search, and it stays linear regardless of the size of the search size.

These graphs go up to 100M set size. Never once did the average number of iterations for Prolly go about 4.9. I ran the test on a 1B sample test, and the number of iterations was actually 5.1. So... I don't think I can claim it's provably constant time, but I'll take it anyway.

Pitfalls

You may be asking, "Why don't we use Prolly search all the time?!", and the reason is that most data isn't uniformly distributed. For example, if you had a group people's ages stored this way, no one would expect there to be an even distribution. Dolt is able to do this in this particular situation because we are looking at cryptographic checksums. Cryptographic checksums, by design, are uniformly distributed.

Also, if you have pockets of dense data, the algorithm regresses to O(N) performance - which is much worse than the rock solid behavior of O(log2(N)). Binary Search turns out to be remarkably resilient to lousy distribution in data. That's why it's been the work horse of the database industry for many decades. Every search index you've ever used uses Binary Search, and will prolly continue to as well.

In Closing

Dolt's use of content address objects gives it some interesting properties. We've talked a lot about Prolly Trees on our blog, and they are only possible due to the value distribution you get with crypto checksums. Hop on Discord to talk about what you got nerd sniped by today!