How Dolt Stores Table Data
Dolt is Git for data. It's a SQL database that lets you clone, branch, diff, merge, and fork your data just like you can with a filesystem tree in Git. This blog post explores one of the fundamental datastructures that underlies Dolt's implementation of SQL tables.
What We Need
Dolt currently supports a
subset of SQL where every table must have a primary key. The SQL layer
is implemented on top of a table storage layer that models a key-value
store, where keys and values are both byte arrays. To efficiently
implement the Git for data portions of
Dolt, we need certain unique
properties from this storage layer. In particular, if the storage
layer models map<byte[], byte[]>, then we would like:
-
A given
map<byte[], byte[]>value should be content addressed. -
The content address of a given
map<byte[], byte[]>should be the same regardless of how the value was built — what sequence of inserts, updates and deletes were used to build the value. -
It should be efficient to diff two
map<byte[], byte[]>values to quickly find entries which are different between two values. -
With content-addressed values, applying mutations like updates, inserts and deletes means that you build a new value. The storage requirements for storing two values, one of which is a mutation of the other, should be proportional to the amount of data that changed between the two values.
-
The amount of structural sharing between two map values should be path-independent, i.e. it should not depend on the sequence of edits which built either map.
The data structure that allows the storage layer to achieve these properties in Dolt is called a Prolly-tree. We first encountered Prolly-trees when we were investigating Noms and we quickly realized how powerful they were for what we were trying to build. A Prolly-tree is a block-oriented search tree that combines the properties of a B-tree and a merkle tree. It uses a clever approach to forming variable-sized blocks in order to optimize for structural sharing and to minimize write amplification on small mutations.
B-tree Review
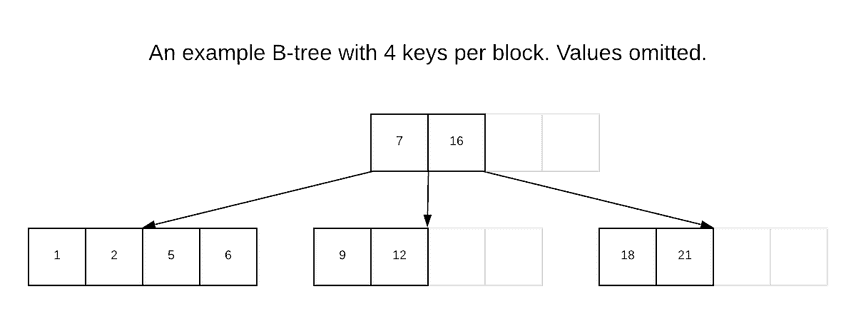
A Prolly-tree somewhat resembles a B-tree, and so we will quickly review those. Recall that a B-tree is block-oriented data structure that maps keys to values. A B-tree stores key-value pairs in leaf nodes in sorted order. Internal nodes of a B-tree store pointers to children nodes and key delimiters; everything reachable from a pointer to a child node falls within a range of key values corresponding to the key delimiters before and after that pointer within the internal node. The end result looks like this:
A B-tree is optimized for a tradeoff between write and read performance — it's more expensive to maintain than just dropping tuples into a heap without any ordering constraints, but when data is stored in a B-tree it's much quicker to seek to a given key and to do an in-order traversal of the keys with their values.
SQL databases often use B-trees, or variants of them, to implement ordered indexes. In some databases, tuples are stored unordered on a heap and a B-tree index is maintained where the values are pointers to matching tuples on the heap. A database can also choose to store the table data directly in an index structure such as a B-tree, which is sometimes called a clustered index. Dolt currently stores all row data directly in the Prolly-tree index corresponding to primary key of the table.
Prolly-trees
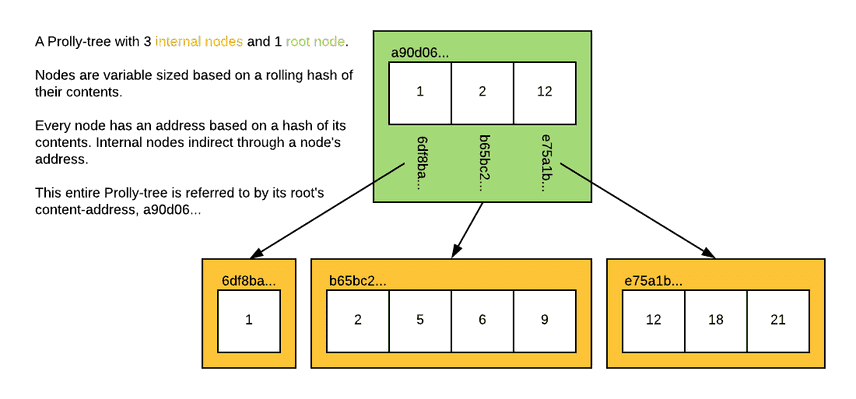
A Prolly-tree is a little like a complete B-tree, but blended with ideas that come from storage algorithms for file sharing and distributed version control systems. A Prolly-tree stores all key-value data in leaf nodes, exactly like a B-tree, and internal nodes with key delimiters and children pointers, exactly like a B-tree. But both the leaf nodes and the internal nodes are variable-length and content-addressed. The children pointers within the internal nodes are the content addresses of the leaf or internal blocks that they point to.
The trick is to pick block boundaries that give us lots of structural
sharing. Intuitively, if we have a map<Date, Float> of all the
temperatures in Los Angeles for the months of Jan, Feb, April, and May
of the year 2019, we want almost no blocks to change when we do any of
the following:
- Insert all temperatures for the year 2018.
- Insert all temperatures for the remainder of the year 2019.
- Insert the missing temperatures for March, 2019.
In order to accomplish that, we can't just use fixed-size blocks and build up a complete content-addressed B-tree with the set of data that we have. Inserting data into one block in the middle of the tree will cause a cascading effect that causes every block that comes after that block to change as well. And that change will ripple up the internal nodes of the tree.
Instead, block boundaries for leaves and internal nodes alike are chosen probabilistically by a rolling hash of the contents of the node itself. The contents of the node are fed to a rolling hash and if the hash value falls below a chosen threshold, a block boundary is formed and a new block is started. The threshold probability for creating a block boundary is set to generate an average desired block size, currently 4KB. But any particular block could be quite small or quite large. The B-tree from above might look like this as a Prolly-tree:
The effect is that the blocks generated by a local mutation to the tree have a very high probability of synchronizing back up with the blocks from the unmutated tree. As soon as the blocks at one layer of the tree are synchronized, the next layer of internal nodes are likely to synchronize as well. In practice, the rolling window can be quite small and many small mutations do not affect chunk boundaries at all. This means that the tree can achieve close to the optimal copy-on-write performance of just replacing the single leaf and the internal nodes that appear on the spline from the leaf to the root internal node of the Prolly-tree.
Naively Building a Prolly-tree
Perhaps the easiest way to conceptualize the end result of building a
prolly tree is to think about a process to build it from the bottom
up. Imagine you have all the <byte[], byte[]> pairs you want to
store in a Prolly-tree.
-
Sort them all by their key value, so that they're laid out in order and place them one after another into a single
byte[]. For the tree above, we would have:
-
Group the resulting byte stream into blocks by running a rolling hash over its contents. Anytime the hash value is below a target value, form a block boundary as soon as you are at the end of a value and start a new block. Here's the blocking step on our leaf nodes:

-
You now have a
list<byte[]>of the leaf nodes of your Prolly-tree. You can compute the content address of each block by applying a strong hash function to its contents. You can store the contents in a content-addressable block store, retrievable atADDR. Here our blocks have been addressed and stored in the block store: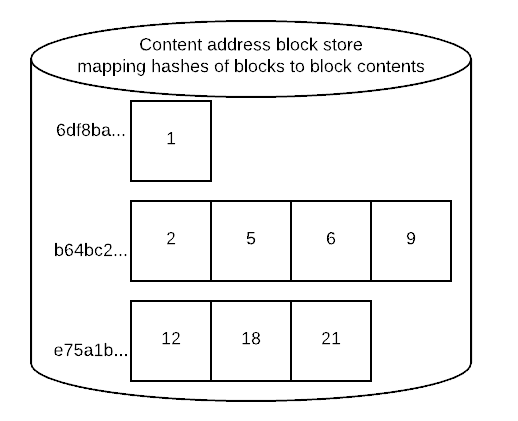
-
If the length of this
listis1, then you are done. The content-address of your table is theADDRof the one block in the list. -
Otherwise, form the next layer of your prolly tree by creating a byte stream that stores
<byte[], ADDR>of every entry in the leaf node list, wherebyte[]is the value of the key in the first entry of the block. Here's what the entries for the first internal level of the tree would look like for our example: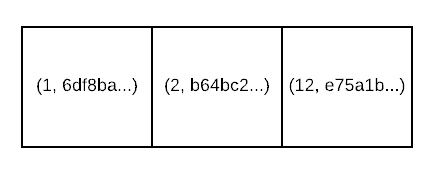
-
If you place those pairs one after another into a single
byte[], you now have a byte stream that can to be turned into content-address blocks to form a layer of internal blocks of your Prolly-tree. To do so, goto step #2. The algorithm terminates when step #4's condition is reached.
Properties of the Prolly-tree
So what can we do with the Prolly-tree given the content addressing and structural sharing?
-
The Prolly-tree for a
map<byte[], byte[]>value forms a merkle tree. We can verify the content addresses of every block, and we have efficient structural sharing without trust issues regarding the contents of the block data itself. -
We have efficient recursive diff between two values. If the content address of two nodes are different, then at least some of the values in the children of that node are different. By comparing content addresses at every layer of the tree, you can quickly walk to just the parts that are different.
-
Similarly, we have an efficient way to synchronize the missing parts of a tree to another repository — as you walk the chunks you need to transit, if you encounter a chunk that is already present in the destination, you don't need to check for the presence of any of its children.
Dolt forms a merkle tree with all repository data, and in particular with commits, and so the synchronization algorithm is entirely data-structure agnostic. But the fact that the table storage itself forms a merkle tree that exhibits a high degree of structural sharing across common changes is very important to Dolt's feasibility.
While the Prolly-tree gives us a lot of nice things, this structure isn't without tradeoffs. Here are some:
-
Variable length blocks are typically not as efficient as an optimally sized fixed-size block for I/O subsystems, allocators, etc.
-
While small changes to a block often don't affect block boundaries, they do change existing boundaries sometimes. Dolt necessarily writes more blocks than even a copy-on-write B-tree implementation.
-
Going through a content-address for internal node pointers means going through another index to find the actual block data. We can't embed pointers in internal nodes within Dolt table storage that allow a direct I/O for the next needed piece of data. While indexes for locating blocks by their addresses can be made quite fast, they're never as fast as having a file offset to a fixed size block directly in hand after reading the internal node, for example.
Conclusion
In conclusion, the Prolly-tree is at the heart of Dolt's ability to efficiently implement Git functionality, such as branch, merge, and diff, for relational data with SQL semantics. Dolt's storage layer blends the concepts of traditional relational database engines with those of distributed version control systems and the result is powerful. We hope you'll take Dolt for a test drive today to see the functionality we've built on top of Prolly-trees.
Further Reading
The Prolly-tree is an interesting combination of a few different ideas from different domains. It works really well for storing structured data with git-like semantics. Check out the following resources to better understand some of the ideas behind the Prolly-tree:
-
Dolt's storage layer is based on Noms, which is where our Prolly-trees came from. Take a look at Nom's take on Prolly-trees, which has recently been updated to explain their properties and implementation in Noms really well.
-
Read up on the wikipedia articles for Merkle trees and B-trees
-
For a description of rolling hashes being used in a file-sharing context to achieve structural sharing, see Lennart Poettering's blog on casync.